Välkomna till Statistikbloggen!
Jag läste en fråga på Facebookgruppen ”Stickcafé” som handlade om hur många gånger man ska kontrollräkna maskorna på sin stickning. Så – i ett försök att bredda läsekretsen – tänkte jag försöka ge lite synpunkter på detta.
Om man stickar måste man (om man är lika amatörmässig som jag i alla fall) kontrollräkna antalet maskor med jämna mellanrum. Om antalet är för litet har man sannolikt tappat en maska som man i så fall måste leta upp och sticka in, men man kan även råkat lägga till en. Ska man sticka en resår vållar detta stora problem eftersom man ska sticka varannan avig, varannan rät och om man har ett fel så blir det både snett och vint.
Så därför måste man ibland kontrollera antalet.
Antag att vi stickar en vante (eller socka) med 40 maskor per varv, fördelade på 4 stickor med 10 vardera. För enkelhets skull antar vi att det är fråga om slätstickning så det är bara räta maskor hela varvet runt. Nu ska vi kontrollräkna antalet…
För varje maska kan vi göra två fel: Missa att räkna (antalet minskar med ett), räkna dubbelt (antalet ökar med ett) eller räkna rätt. Vi betecknar dessa med (-1, +1 respektive 0). Gör vi alla rätt kommer vi att få rätt svar. Men hur kan vi veta att vi faktiskt har rätt bara för att vi får rätt summa? Vi kan ju ha räknat fel två gånger!
Inom informationsteori talar man om felupptäckande och felrättande koder. En upptäckande kod innehåller en kontrollmöjlighet som gör att vi kan upptäcka vissa fel, men vi kan inte rätta dem. Exempel på detta är kontrollsiffran i personnumren och OCR-numren. Man kan se att det är fel på ett personnummer om kontrollsiffran är fel, men man kan inte se vad det rätta numret är. En rättande kod så kan man även korrigera felet så att det blir rätt. Men om två siffror ändras samtidigt så kan kontrollsiffran bli rätt i alla fall och felet går obemärkt förbi…
Ett exempel på en felupptäckande kod inom stickning är att om man stickar resår (varannan rät och varannan avig). Om sista maskan blir rät vet man att det är fel någonstans, men inte var eller hur detta ska korrigeras. Men även här kommer två fel att ta ut varandra.
Låt oss anta att du oftast räknar rätt. Säg att felräkningar inträffar 1 gång på 1000 (var 1000:e maska missas ELLER dubbleras, medan 999 räknas rätt). Det betyder att en kontrollräkning av vanten ovan kommer att ha noll fel med en sannolikhet på 96,1%. Sannolikheten för EXAKT ett fel är 3,8% och sannolikheten för MINST 2 fel är 0,076%. Se tabellen nedan.
Men även om man gör minst 2 fel så kan det fortfarande vara så att felräkningarna syns. Ett udda antal fel kommer t.ex. alltid att synas. Likaså om samma fel görs fler gånger (man missar t.ex. att räkna 2 maskor). Gör man däremot fel så kommer det att vara ETT fel eller ett antal fel som syns i alla fall med mycket hög sannolikhet (över 99%). Så om man bara gör fel 1 gång på 1000 så kommer man med största sannolikhet att få rätt resultat, d.v.s. upptäcka ett fel som finns eller godkänna ett korrekt arbete. Ett räknefel kommer alltså inte att gå att missa.
Om du är slarvigare och gör fel på var hundrade maska så blir kontrollräkningarna trots det rätt med en sannolikhet på 67%. Även i detta fall kommer det att vara mycket sannolikt att OM man gör ett fel så är det bara ett fel (81,7%).
Men slarvar man ännu mer och gör fel på var 10:e maska så blir det problem. Då kan man troligen inte lita på sin kontrollräkning alls utan måste kontrollräkna flera gånger oavsett resultat.
Jag tror att de flesta med lite noggrannhet kommer att räkna rätt så ofta att om man gjort fel så upptäcks detta. Kontrollera gärna själv genom att räkna samma stycke flera gånger. Därför drar jag slutsatsen att om man stickar vantar eller raggsockor så ska EN genomräkning räcka. Skulle det bli ett felaktigt antal så måste man gå igenom arbetet en gång för att finna felet, som sannolikt kommer att finnas.
Hälsningar
Magnus
Tack till Monica Larsson som gav mig inspiration till denna bloggpost!
Välkommen till statistikens underbara värld! En blogg för dig som är intresserad av statstik till vardag och fest. Ingen siffra är för obskyr, ingen händelse för otrolig, ingen datamängd för stor eller liten. Ingen tanke eller fenomen som inte kan illustreras i siffror!
onsdag 20 augusti 2014
måndag 12 maj 2014
Nicholas Cage och drunkningsdöden
Hej Statistikvänner!
Jag fick ett kul länktips av min kompis Torsten Beckman (http://www.tylervigen.com/).
Siten presenterar 20 stycken korta tidsserier där det finns
en tydlig korrelation mellan några – väldigt märkliga. Bland annat är det så
att fler drunknar i swimmingpoolar de år då det kommer ut fler filmer med
Nicholas Cage. Man kan fundera länge över hur detta kommer sig, men svaret är
lika enkelt som tråkigt.
 |
| Nicholas Cage - The man, the myth, the statistic |
Bara för att det finns en korrelation i data så har man inte
automatiskt ett orsakssamband. Det är alltså inte så att Nicholas Cages agent
arbetar mer aktivt om folk drunknar. Lika lite tror jag att hans filmer får
folk att drunkna – varken avsiktligt eller oavsiktligt.
Ibland finns det en effekt som kallas ”skensamband”. Bakom
två variabler ligger en tredje som man inte tittar på. Det finns ett logiskt
samband mellan denna och bägge de andra, men inte mellan de man betraktar… Om
du inte hängde med: Det finns bevis för att kaffedrickare oftare får
lungcancer. Orsaken till detta är att rökare BÅDE dricker mer kaffe och får
lungcancer, inget annat. Jag gillar inte att vara kategorisk, men jag tror inte
att det finns någon tredje faktor som ger Nicholas Cage filmkontrakt och får
folk att drunkna.
Svaret ligger i att dataserien är kort (11 år) och att de är
många.
Jag roade mig med att göra en simulering på helt oberoende
data upprepat 20 gånger. Den bästa av körningarna hade en
korrelationskoefficient på 0,54 se figuren. Faktum är att om man gör om samma
sak med bara 5 serier som testas i alla par som är möjliga (20 st) så blir det
65% i det bästa fallet.
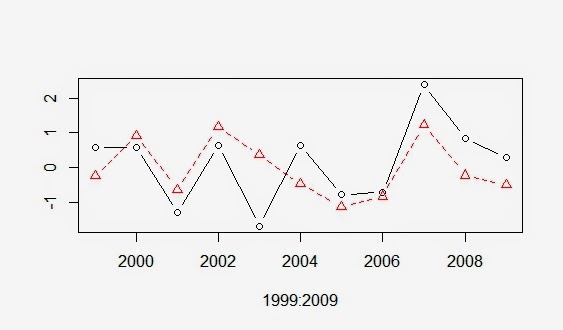 |
| Simulerade data för 1999 till 2009. Helt oberoende... Trots det blev det en fin korrelation. |
De har presenterat 20 resultat, sammanlagt 40 variabler. Antalet
möjliga par är 780 stycken. Det är inte konstigt att det finns de med hög
korrelation.
Man bör vara
försiktig med att tolka denna ”information” eftersom det kan leda till
felaktiga slutsatser. Dessa slutsatser kan i sin tur orsaka stora skador. Man
skulle behöva en varningstext som de som sitter på cigarettpaketen. ”Varning –
Dålig statistik kan skada dig allvarligt!”.
onsdag 22 januari 2014
Facebook dör ut mellan 2015-17
Hej,
Facebook på väg att dö ut som en smittsam sjukdom! Få saker
väcker ett intresse som en bra rubrik.
Inom statistiken använder man modeller, d.v.s. en förenklad
bild av hur verkligheten fungerar. I modellen finns slumpmässiga förlopp,
påverkan m.m. inlagda och sedan skattar man hur stora dessa är.
Inom epidemiologi – läran om smittsamma sjukdomars spridning
– finns en enkel modell som delar in alla människor i tre faser: Mottaglig,
Smittad, Resistent. Först kan man bli smittad av sjukdomen, sedan är man
smittad och sprider smittan vidare till andra mottagliga och sedan blir man
Resistent mot smitta. Till detta finns mängder av variationer. T.ex. kan
resistent betyda att man avlidit.
På engelska kallas detta ”SIR”-modellen (Susceptible, Infected,
Resistent).
Beroende på hur lätt det är att smitta andra och hur ofta
detta sker och hur lång tid smittade har på sig att sprida sjukdomen vidare
blir det olika förlopp. Rabies och hiv sprids ganska sakta eftersom smittotillfällena
är få. Å andra sidan influensa sprids snabbt och kan explodera i pandemier för
att sedan dö ut då stora delar av befolkningen utsatts för smittan och antingen
blivit immuna eller dött.
Forskare vid Princeton University [1] har tillämpat samma
modell på Facebook. Man kan betrakta en person utan Facebook-konto som ”Mottaglig
för smitta”, en som anslutits som ”smittad”. Om man tillämpar denna modell kan
man se hur snabbt farsoten sprider sig innan en pandemi mer eller mindre brutit
ut. Men de har även beräknat att trenden vänder och denna vändning finns med i
modellen.
Likt spanska sjukan och böldpesten kommer smittan att
avklinga. Enligt forskarna har detta redan skett med MySpace som följde samma
mönster för några år sedan. Facebook nådde sin topp 2012 och kommer att tappa
80% av sina användare mellan 2015 och 2017.
[1] J
Cannarella and J A Specler (2014). Epidemiological modeling of online social
network dynamics. http://arxiv.org/pdf/1401.4208v1.pdf
Prenumerera på:
Kommentarer (Atom)

